Okay, here's where we get into somewhat science-fictiony territory (what, the giant robots and blaster pistols weren't enough SciFi?), and consider what happens on space stations that use spin to simulate gravity. Before we talk about frame effects, though, I should briefly explain how this works in the first place, for people who are hazy on the concept. Spin-Simulated Gravity     In a zero-gravity or free-fall (i.e. orbital) environment, there's no well-defined "down" to let you stand on a floor. Instead, everything drifts, either because there's no force acting on it, or because everything's falling around in orbit at the same rate...when the floor's falling as fast as you are, it's hard to stay on the floor.     However, Newton's First Law is still in effect. If you get something moving, it will want to keep moving, and require a force to change its speed or direction. If you can move something in a circle, then you'll have a force pulling it towards the center of that circle. So, in the picture to the right, the figure would tend to go in a straight line shown by the blue arrow, but the floor is pushing up on it with a force shown by the orange arrow, curving his path into a circle.     On Earth, gravity pulls us down, and the force of the floor pushes up equally hard, to keep us from falling. But we don't directly feel gravity, we just feel the push up from the floor. Since the floor's pushing up in this rotating space station, the figure feels like there's gravity, since that familiar push of the floor is there.     The amount of that push is determined by the square of how fast the station spins in rotations per second, and how far out you are. To throw out an equation for those who like such things, Fcentripetal = ω²r     So, at first blush, as long as the station spins fast enough and you're far enough out from the axis of rotation, you have enough gravity to go about your business. Of course, this isn't actually gravity, and there's some funky complications. Complication 1: Too Small!     One of the problems of spin-simulated gravity is that pesky r term above. No one is a point mass, and your head and feet will be at different radii. If you're in a rotating cylinder with a radius only slightly bigger than your height, then your head and feet will be moving at noticeably different speeds, as seen in the picture to the right. The blue arrows representing speed at a given radius are quite different at head level and at foot level.     This alone may only be disorienting, but it also means that if you move even a little, the effective "down" direction will be different for different parts of your body...good luck staying on your feet! Additionally, any contribution to frame effects from the Corilis force will be worse when the chamber is small, since Coriolis is all about changes of speed in a rotating system. Generally, unless the chamber is several times wider than your height, it's really only good for lying down in to sleep in gravity. Complication 2: Straight Lines     Remember, this isn't really gravity. Once you're no longer touching a surface, there's no force on you at all, and you'll travel in a straight line while the ground moves under you. If you were to jump straight up, you'd be adding your jump speed to your spin-related speed and fly off at an angle, as shown on the figure to the left. Odds are pretty good that you'd end up drifting spinward, since you'd be "cutting the corner" as well as traveling faster overall than the ground (ground speed plus your jump speed will be greater than the ground speed), and you'll hit with a speed spinward with respect to the ground. Jump up, come down sideways. Yes, this is a frame effect, just one of many.     The picture to the left illustrates this.     In frame 1, we have a robot jumping straight up. The blue arrow now represents his upward speed, and the yellow arrow is the spin speed. The green arrow is how fast and in what direction he's going after leaving the floor (a "vector sum" of the blue and yellow arrows).     Frame 2 is a little busy, but here's what's going on. Orange arrow A points to the takeoff spot at zero seconds (initial time), where the robot was when he jumped up. Now, if the green arrow is a speed in meters per second, then it takes him two seconds (two green arrows) to hit the floor again. In two seconds, the takeoff spot has moved by two yellow arrows. So, orange arrow B points to where the takeoff spot has moved to, and orange arrow C points to where the robot actually landed.     Frame 3 cleans up the "after two seconds" picture a little. The new blue arrow placed outside the station shows how far the robot has drifted "spinward" during his jump. Notice, too, that his head is still pointed in the same direction as when he jumped up, but on landing he's practically sideways to the ground!     In short, if you can jump up with a speed even close to the speed at which the ground is moving, you'll not only not come "straight back down," you're also likely to come down at an awkward angle. Robots jumping around inside space stations had better have good gyroscopes and maneuvering thrusters if they don't want to embarrass themselves. Complication 3: Frame Effects In General     Any time you try to move towards or away from the axis of rotation, as seen in the picture to the right, your speed will no longer match the speed of your surroundings. If you move towards the axis, you will move faster in the spinward direction than the ground below you, making ramps and stairs a tricky proposition. If you move away from the axis, you'll be slower than the ground below you, also fun at parties. On ramps or stairs, it'll feel like the ground is speeding up or slowing down. On an elevator or ladder moving directly along the radius, you'll feel forced to one side or another. This can get old really fast. In a smaller rotating chamber, even the act of sitting down or standing up too quickly could cause you to tip over sideways!     In the picture to the right, as the robot drops down a level, the ground below him moves faster than the spin direction he started with, so he drifts "anti-spinward" as he goes down. In free dropping, this just means he lands in the wrong place. If he's going down a solid tube, it means he's pushed up against the anti-spinward wall the whole time.     Staying at a constant radius doesn't eliminate your troubles either. If you move in the same direction as spin, you increase your personal ω and feel heavier...go too fast and you won't be able to stand at all! If you move against the spin, you could potentially come to a standstill and start to float while the ground rushes by under you, although the wind would quickly slow you down enough to regain your footing. Still, having your weight change depending on which direction you move is going to make for treacherous footing. And keep in mind that walking is not exactly a constant radius proposition, you tend to bounce up and down a little, which will only make things worse if you have a small-radius, high-speed chamber.     In the picture to the left, the robot starts running anti-spinward with a speed represented by the right-pointing yellow arrow. On the other hand, the ground moves spinward at the speed of the left-pointing yellow arrow. At just the right speed, the robot comes to a complete halt with respect to space outside the station, and no longer has any force pushing him up towards the axis. So he floats for a bit until the wind reduces his speed. Hopefully he's not doing this in an airless station....     As an aside, I initially didn't link in this cartoon (which I've had on my office door for several years now) because it's actually using Newton's First Law incorrectly. But a lot of people have seen it, so I'm linking it now so I won't get more people "bringing it to my attention". :) I'll leave it as an exercise to the reader to figure out the two reasons (one major, one minor) why things shouldn't work like they're shown in the cartoon.     Most of these problems can be minimized by having everything at a constant radius (large open space down the middle of the space station) and spinning quickly enough that you're not going to catch up to the spin rate. For an inner surface of 10 meters radius, a station spinning once every five or six seconds will simulate a comfortable fake gravity, and you'd have to sprint before you'd start noticing changes in your effective weight. So obey those "no running" signs! Types of Space Stations     In order to use spin to simulate gravity, you need some sort of shape that cna be rotated without coming out of balance. You also need to arrange things so that "up" is always towards the center of this rotation. This leaves out a lot of shapes seen in science fiction, which (if hard SF) just have no artificial gravity at all, or (if not so hard SF) use handwave science to allow gravity without spin. In between, you can have colony ships that accelerate steadily half the way to their destination, then turn around and decelerate the rest of the way. We're going to ignore all of those and concentrate on the ones that spin to simulate gravity.     The O'Neill Cylinder is perhaps the most spacious and least tricky-to-live-in style of rotating station. The diagram to the left is a very basic depiction of one, there's plenty of variations on the theme. In a classic "can" station, all the habitation is confined to a narrow band of nearly constant radius, although the entire interior is filled with air. It's large and relatively slow-spinning, with a radius of perhaps 100 meters, requiring a rotation of once every 20 seconds to get "Earth normal" gravity on the shell. For such an O'Neill, the spin speed of the ground would be over sixty miles per hour, so foot traffic wouldn't need to worry about weird gravity effects, and vehicles would either be on rails or have other limiters to prevent excessive speed.     A classic can is hollow down the center and that space is not used by people, although it might have automatic systems or even low-grav recreation areas along part of it. Getting to and from the axial section presents some challenges, which will be discussed in the "Spoked Wheel" station later.   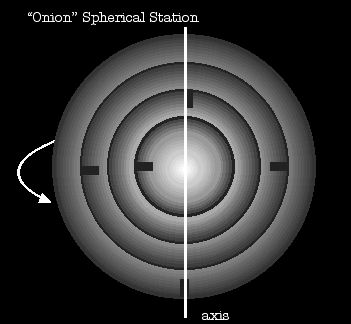  While spherical stations usually use handwave artificial gravity, some stories have spinning spheres. The reasoning is that it's a lot easier to keep a sphere pressurized than a cylinder, for purely structural reasons. They're often built in an onion-layer fashion to maximize use of the volume...if you're worried about the inefficiency of an O'Neill, you're probably scraping for space.     On the small scale, while it may have onion layers for structural integrity, the actual structures inside will be built so that "up" is the axis of rotation, not the center of the sphere. The best residential real estate will be found in the outer layer at the equator, whereas anything near the axis will be reserved for purposes where low acceleration is either acceptable or even desired. However, getting from one place to another will invoke all sorts of frame effects, as Asimov once investigated in a short story the title of which escapes me now.     A hybrid is certainly possible, in which a cylinder is nestled inside a sphere. The cylinder would act like a typical O'Neill can, while the higher "gravity" sections between the outer wall of the cylinder and the sphere would be reserved for things that don't require as much human presence.   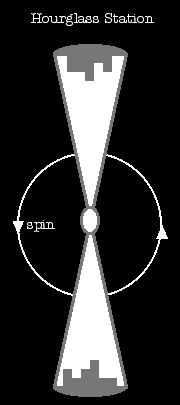  If you want the benefit of an O'Neill's stability but don't have the resources for a full cylinder, one option that's been seen in science fiction is the hourglass. The central hub would contain anything that favors low acceleration, and travel between the two halves would be really unpleasant unless done slowly. As a result, the halves might function as independent entities, or one half might be dedicated more to automated systems or other things that require minimal human attention. It could even be left evacuated to save on air.     The hourglass plan is also applicable to spaceships that have a rotating section to simulate gravity, but aren't big enough to just have an internal ring or cylinder. The hourglass or barbell shape spins around at some place on the ship's axis, providing limited gravity simulation. However, this can cause problems for maneuvering, and odds are there isn't enough radius to get really stable artificial gravity. In other words, it's a place to lie down or maybe do some exercise, but you won't want to have to work in it.   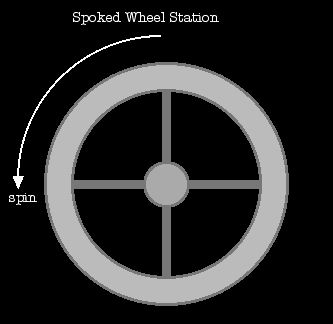  The spoked wheel is the last one I'll present here, but it may well be the first image most people think of when they consider space stations that spin. The main or "habitat" ring is spun quickly enough to provide comfortable gravity, while the hub is at low pseudo-gravity. There may be another ring between the habitat ring and the hub, as well. Travel along the spokes results in Coriolis frame effects, as moving inward has you moving faster than the spoke and smooshing spinward, while moving outward has you moving more slowly than the spoke and smooshing anti-spinward. As a result, while it might be faster to cut across the hub when trying to get to the other side of the station, it's distinctly unpleasant.     An O'Neill may have internal spokes as well, and multiple layers spread out along the whole interior, in which case the spoked wheel model's problems become the O'Neill's problems too. High speed elevators between levels would be quite nasty to ride in, and probably require getting strapped into safety harnesses. Back to the Main Coriolis force Page.