In Quantum Enigma by Rosenbaum and Kuttner, a "stick polarization" example is presented to help explain Bell's Inequality, but in my opinion they don't really clarify what it means to violate the inequality. So the following diagrams are my attempt at explaining that point. There's plenty of other graphical explanations of BI out there, of course, but since I was teaching a course out of Quantum Enigma in Fall 2011, I needed to explain the thing we had.

    Because Word draw is cruddy and the new Apple word processing program is even worse, I loaded up a copy of AppleWorks and used that.

Image 0 - Setup

Image 1 - No disagreement

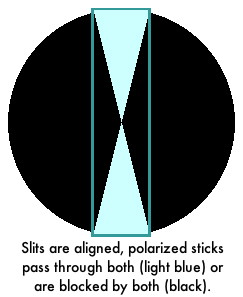
Image 2 - 15° disagreement

Image 3 - 35° disagreement

Image 4 - 90° disagreement

    While real pairs of sticks are (as far as we can tell) seperable, and the 90 degree case would not be any worse than the 35 degree case, experiments with pairs of polarized photons have shown entanglement.

    In other words, two photons created in such a way that we know they need to have the same polarization (but don't know what that value is from the beginning) will somehow share information at faster than the speed of light, so that measuring one of them will create the value of polarization in the other.

   Yeah, quantum mechanics are weird. Don't even get me started on the Ithaca Interpretation of Quantum Mechanics....

Back to the Opera of the Dvandom